LeetCode 题解（思路归纳）

1. 所有题目来源为力扣
2. 题解为原创，仅为个人当前阶段能想到/能接受的解法，不一定是优解
3. 🟢简单 🟠中等 🔴困难 ⚪未完成 ⚫未更新

链表

🟠 92. 反转链表 II

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

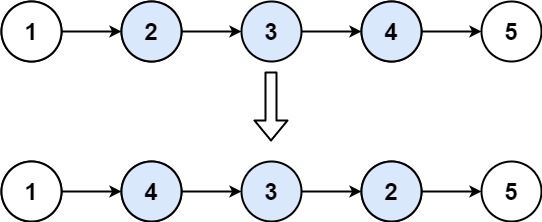
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

示例 2：

输入：head = [5], left = 1, right = 1
输出：[5]

题解

分三步走即可。

1. 将用于遍历的指针 p 定位到要反转的 section 头节点处，同时跟踪到 section 头节点的前一个节点，记作 pBeforeMiddle；
2. 使用头插法将 section 内的 right-left+1 个节点插入一个新的链表中，完成反转需求。注意第一个进行头插的节点 firstHeadInserted 会成为反转后的最后一个节点，为了将反转 section 接上后续不用反转的部分，第一个进行头插的节点要用指针存一下；
3. 将 pBeforeMiddle 节点接上 section 的第一个节点，同时将 firstHeadInserted 接上 section 后面的那个节点即可。

完整代码：

public class Solution {
    public ListNode ReverseBetween(ListNode head, int left, int right) {
        ListNode p = head;
        ListNode pBeforeMiddle = null;
        ListNode middleList = new ListNode(-1, null);
        // locate the node before section need to reverse
        for(int i = 1; i < left; i++)
        {
            pBeforeMiddle = p;
            p = p.next;
        }
        // now, p point the first node of the section need to reverse
        // head insert to reverse the section
        // save firstHeadInserted for connect the rest nodes after reverse section
        ListNode firstHeadInserted = new ListNode(p.val, null);
        middleList.next = firstHeadInserted;
        p = p.next;
        for(int i = 1; i < right - left + 1; i++)
        {
            middleList.next = new ListNode(p.val, middleList.next);
            p = p.next;
        }
        // connect the rest nodes after the reversed section
        firstHeadInserted.next = p;
        if(pBeforeMiddle != null) 
        {
            pBeforeMiddle.next = middleList.next;
            return head;
        } else return middleList.next;
    }
}

🟠 86. 分隔链表

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当 保留 两个分区中每个节点的初始相对位置。

示例 1：

输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

提示：

• 链表中节点的数目在范围 [0, 200] 内
• -100 <= Node.val <= 100
• -200 <= x <= 200

题解

应是简单题。遍历链表，按顺序将小于 x 和大于等于 x 的节点分别收集到两个链表中，最后将两个链表相接即可实现相对位置不变的链表分隔。

完整代码：

public class Solution {
    public ListNode Partition(ListNode head, int x) {
        if(null == head) return head;
        ListNode p = head;
        ListNode smallerList = new ListNode(-1, null);
        ListNode bigList = new ListNode(-1, null);
        ListNode smallerP = smallerList, bigP = bigList;
        while(p != null)
        {
            ListNode node = new ListNode(p.val, null);
            if(p.val < x) { smallerP.next = node; smallerP = smallerP.next; }
            else { bigP.next = node; bigP = bigP.next; }
            p = p.next;
        }
        smallerP.next = bigList.next;
        return smallerList.next;
    }
}

---

动态规划 / 记忆化搜索

🔴 403. 青蛙过河

一只青蛙想要过河。 假定河流被等分为若干个单元格，并且在每一个单元格内都有可能放有一块石子（也有可能没有）。 青蛙可以跳上石子，但是不可以跳入水中。

给你石子的位置列表 stones（用单元格序号 升序 表示）， 请判定青蛙能否成功过河（即能否在最后一步跳至最后一块石子上）。

开始时， 青蛙默认已站在第一块石子上，并可以假定它第一步只能跳跃一个单位（即只能从单元格 1 跳至单元格 2 ）。

如果青蛙上一步跳跃了 k 个单位，那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意，青蛙只能向前方（终点的方向）跳跃。

示例 1：

输入：stones = [0,1,3,5,6,8,12,17]
输出：true
解释：青蛙可以成功过河，按照如下方案跳跃：跳 1 个单位到第 2 块石子, 然后跳 2 个单位到第 3 块石子, 接着 跳 2 个单位到第 4 块石子, 然后跳 3 个单位到第 6 块石子, 跳 4 个单位到第 7 块石子, 最后，跳 5 个单位到第 8 个石子（即最后一块石子）。

示例 2：

输入：stones = [0,1,2,3,4,8,9,11]
输出：false
解释：这是因为第 5 和第 6 个石子之间的间距太大，没有可选的方案供青蛙跳跃过去。

提示：

• 2 <= stones.length <= 2000
• 0 <= stones[i] <= 231 - 1
• stones[0] == 0

题解

通过直觉，不难想到回溯遍历的方式找到可能的到达终点的路径。对于青蛙的任意状态，都能够由当前石头下标 currentI 和由上一块石头经过几跳 lastJump 到达当前石头这么两个参数确定，由于青蛙下一跳只能跳 lastJump-1 ~ lastJump+1 跳，故从 stone[] 中向后找能恰用这些步数到达的石头进行转移，若没有石头可以转移，说明该路径不能到达终点。

完整代码：

class Solution {
    boolean can;
    public boolean canCross(int[] stones) {
        can = false;
        try2Cross(stones, 0, 0);
        return can;
    }
    public boolean try2Cross(int[] stones, int currentI, int lastJump) {
        if(currentI == stones.length - 1 || can) { can = true; return true; }
        boolean canReach = false;
        for(int i = currentI+1; i < stones.length; i++) {
            int distance = stones[i] - stones[currentI];
            if(distance > lastJump + 1) break;
            if(distance == lastJump - 1) { canReach |= try2Cross(stones, i, lastJump-1); }
            else if(distance == lastJump) { canReach |= try2Cross(stones, i, lastJump); }
            else if(distance == lastJump + 1) { canReach |= try2Cross(stones, i, lastJump+1); }
        }
        if(canReach) return true;
        return false;
    }
}

虽然在用例计算量较小时可以通过，但对于递归较深重复很多的情况下会超时，故用记忆化搜索优化之，易得：

class Solution {
    boolean can;
    HashMap<String, Integer> mem;
    public boolean canCross(int[] stones) {
        can = false;
        mem = new HashMap<>();
        try2Cross(stones, 0, 0);
        return can;
    }
    public boolean try2Cross(int[] stones, int currentI, int lastJump) {
        if(currentI == stones.length - 1 || can) { can = true; return true; }
        String key = String.valueOf(currentI) + " " + String.valueOf(lastJump);
        if(mem.getOrDefault(key, -1)==0) return false;
        boolean canReach = false;
        for(int i = currentI+1; i < stones.length; i++) {
            int distance = stones[i] - stones[currentI];
            if(distance > lastJump + 1) break;
            if(distance == lastJump - 1) { canReach |= try2Cross(stones, i, lastJump-1); }
            else if(distance == lastJump) { canReach |= try2Cross(stones, i, lastJump); }
            else if(distance == lastJump + 1) { canReach |= try2Cross(stones, i, lastJump+1); }
        }
        if(canReach) return true;
        mem.put(key, 0);
        return false;
    }
}

🟢 70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

题解

首先很容易想到回溯遍历，每种状态都 DFS 往下找走一步和走两步的情况，直到 n 耗尽，就不重不漏地找到了所有路径。

class Solution {
    int res = 0;
    public int climbStairs(int n) {
        res = 0;
        climb(n);
        return res;        
    }
    public void climb(int leftN) {
        if(leftN <= 0) {
            res++; return;
        }
        climb(leftN - 1);
        if(leftN > 1) climb(leftN - 2);
    }
}

不过稍微测试一个大一点的用例，比如输入 42，执行结果就超时了，因此我们需要思考一下进行优化。

虽然挺久没有做到记忆化搜索的题了，但是很幸运，当提交用例超时的那一瞬间，瞬间就触电般地想到了借助记忆化搜索对该 DFS 剪枝便能完美解决此题。遂改之：

class Solution {
    int res = 0;
    HashMap<Integer, Integer> waysForN;
    public int climbStairs(int n) {
        res = 0;
        waysForN = new HashMap<>();
        climb(n);
        return waysForN.getOrDefault(n, -1);        
    }
    public void climb(int leftN) {
        if(leftN <= 0) { res++; return; }
        int mem = waysForN.getOrDefault(leftN, -1);
        if(mem != -1){ res += mem; return; }
        int oriRes = res;
        climb(leftN - 1);
        if(leftN > 1) climb(leftN - 2);
        waysForN.put(leftN, res - oriRes);
    }
}

用记忆化搜索改进后，从超时到 0ms，顺利 AC 了。

虽然 AC 了，但是想到既然能用记忆化搜索，那不如顺带再用动态规划解一遍吧，就当复习一下动态规划了。

不难定义状态 dp[i] 表示走 i 阶楼梯的情况数，那么同样不难想到， dp[i] 可由 dp[i-1] 和 dp[i-2] 转移得来，因为第 i 阶楼梯可由 i-1 阶楼梯走一步到达，也可由 i-2 阶楼梯走两步到达。故有转移方程 dp[i] = dp[i-1] + dp[i-2]。同时初始状态显然为 dp[0] = dp[1] = 1。

同样 AC 的动态规划解法完整代码：

class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n+1];
        dp[0] = dp[1] = 1;
        for(int i = 2; i <= n; i++) dp[i] = dp[i-1] + dp[i-2];
        return dp[n];
    }
}

🟠 64. 最小路径和

给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

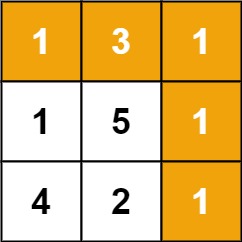
示例 1：

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

题解

• 状态定义：dp[i,j] 表示移动到 (i,j) 处的最小代价。
• 状态转移：
  • 若 i == 0 且 j > 0，则 dp[i,j] = dp[i,j-1] + grid[i][j]，因为只能从左侧转移来；
  • 若 j == 0 且 i > 0，则 dp[i,j] = dp[i-1,j] + grid[i][j]，因为只能从上方转移来；
  • 若 i > 0 且 j > 0 ，则 dp[i,j] = Max(dp[i,j-1],dp[i-1,j]) + grid[i][j] 以满足最小代价。

完整代码：

public class Solution {
    public int MinPathSum(int[][] grid) {
        int m = grid.Length, n = grid[0].Length;
        int[,] dp = new int[m, n];
        dp[0, 0] = grid[0][0];
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(i == 0 && j > 0) dp[i, j] = dp[i, j-1] + grid[i][j];
                if(j == 0 && i > 0) dp[i, j] = dp[i-1, j] + grid[i][j];
                if(i > 0 && j > 0) dp[i, j] = Math.Min(dp[i, j-1], dp[i-1, j]) + grid[i][j];
            }
        }
        return dp[m-1, n-1];
    }
}

🟠 63. 不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

题解

• 状态定义：dp[i,j] 代表移动到 (i,j) 的路径数，且 obstacleGrid[i,j] = 1 的地方 dp[i,j] 必为 0。

• 状态转移：

  • 当 i == 0 且 j > 0 时，dp[i,j] = dp[i,j-1]，即与左边来的路径数一致；

  • 当 j == 0 且 i > 0 时，dp[i,j] = dp[i-1,j]，即与上边来的路径数一致；

  • 当 i > 0 且 j > 0 时，dp[i,j] = dp[i-1,j] + dp[i,j-1]，即从左来的路径数与从上来的路径数之和。

完整代码：

public class Solution {
    public int UniquePathsWithObstacles(int[][] obstacleGrid) {
        if(obstacleGrid[0][0] == 1) return 0;
        int m = obstacleGrid.Length;
        int n = obstacleGrid[0].Length;
        int[,] dp = new int[m, n];
        dp[0, 0] = 1;
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(i == 0 && j > 0) dp[i, j] = obstacleGrid[i][j] == 1 ? 0 : dp[i,j-1];
                if(j == 0 && i > 0) dp[i, j] = obstacleGrid[i][j] == 1 ? 0 : dp[i-1,j];
                if(i > 0 && j > 0) dp[i, j] = obstacleGrid[i][j] == 1 ? 0 : dp[i,j-1] + dp[i-1,j];;
            }
        }
        return dp[m-1, n-1];
    }
}

🟠 62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

题解

• 状态定义：dp[i,j] 代表移动到 (i,j) 的路径数，且显然当 i == 0 或 j == 0 时，路径数量为一条。
• 状态转移：当 i > 0 且 j > 0 时，dp[i,j] = dp[i-1,j] + dp[i,j-1]，即从左来的路径数与从上来的路径数之和。

完整代码：

public class Solution {
    public int UniquePaths(int m, int n) {
        int[,] dp = new int[m, n];
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(i == 0 || j == 0) dp[i, j] = 1;
                else dp[i, j] = dp[i, j-1] + dp[i-1, j];
            }
        }
        return dp[m-1, n-1];
    }
}

🟠 120. 三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

提示：

• 1 <= triangle.length <= 200
• triangle[0].length == 1
• triangle[i].length == triangle[i - 1].length + 1
• -104 <= triangle[i][j] <= 104

题解

• 状态定义：dp[Two2OneDemensional(i,j)] 表示移动到位置 (i,j) 的最小路径和，且显然初始条件为 dp[0] = triangle[0][0]，表示顶点到自己的最短路径和即为自己本身。
• 状态转移：由题意“每一步只能移动到下一行中相邻的结点上”可知，dp[k] 可由上方节点转移来，也可能由左上方节点转移来。不过特别地，最右侧节点只可能由左上方转移来，因为其没有正上方节点；同理最左侧节点只可能由上方转移来，因为其不存在左上方的节点。

题目要返回的是到达三角形底部的最小路径和，因此取底部节点的 dp 中最小的那个即可。

完整代码：

public class Solution {
    public int MinimumTotal(IList<IList<int>> triangle) {
        List<IList<int>> l = new List<IList<int>>(triangle);
        int length = l.Count;
        if(length == 0) return 0;
        int[] dp = new int[(1 + length) * length / 2];
        dp[0] = triangle[0][0];
        for(int i = 1; i < length; i++){
            for(int j = 0; j <= i; j++){
                // 非最右侧，最小路径就可能从头顶上来
                int pathSum1 = (i!=j)?dp[Two2OneDemensional(i-1,j)]+triangle[i][j]:int.MaxValue;
                // 非最左侧，最小路径就可能从左边的头顶上来
                int pathSum2 = (j>0)?dp[Two2OneDemensional(i-1,j-1)]+triangle[i][j]:int.MaxValue;
                dp[Two2OneDemensional(i,j)] = Math.Min(pathSum1,pathSum2);
            }
        }
        int min = int.MaxValue;
        for(int j = 0; j < length; j++){
            int val = dp[Two2OneDemensional(length-1, j)];
            if(val < min) min = val;
        }
        return min;
    }

    public int Two2OneDemensional(int i, int j){
        return (1 + i) * i / 2 + j;
    }
}

🟠 931. 下降路径最小和

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：下面是两条和最小的下降路径，用加粗+斜体标注：
[[2,1,3],      [[2,1,3],
 [6,5,4],       [6,5,4],
 [7,8,9]]       [7,8,9]]

示例 2：

输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：下面是一条和最小的下降路径，用加粗+斜体标注：
[[-19,57],
 [-40,-5]]

示例 3：

输入：matrix = [[-48]]
输出：-48

提示：

• n == matrix.length
• n == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

题解

• 状态定义：dp[i][j] 表示移动到位置 (i,j) 的最小路径和，且显然初始条件为 dp[0][:] = matrix[0][:]，表示第一行各节点到自己的最短路径和即为自己本身。
• 状态转移：由题意可知，dp[k] 可由上方、左上方或右上方节点转移来。不过特别地，最右侧节点只可能由上方或左上方转移来，因为其没有右上方节点；同理最左侧节点只可能由上方或右上方转移来，因为其不存在左上方的节点。

题目要返回的是到达方形底部的最小路径和，因此取底部节点的 dp 中最小的那个即可。

备注：这题和 120. 三角形最小路径和 几乎一样，但在编码本题的时候使用使用了一个空间优化技巧。

考虑到填充到达每层的最短路径时，仅与到达上一层的最短路径相关，与更上方的层无关，因此只需要存储当前层的 dp 值，给下层提供依赖即可，使用 层数&1 的方式来实现只存储到达上一层和当前层的最短路径值，当遍历到下一层时，就自动覆盖之前使用完毕的上层 dp 值，实现滚动数组，复用空间，将 dp[length][length] $O(n^2)$ 的空间复杂度降到了dp[2][length] 的 $O(n)$。

完整代码：

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int length = matrix.length;
        // dp[i][j]: The min path sum of accessing (i,j),
        // but only adjacent layers are meaningful, so use &1
        // to save only 2 adjacent layers' dp data
        int[][] dp = new int[2][length];
        // Initialize dp[][]
        for(int i = 0; i < length; i++){ dp[0][i] = matrix[0][i]; }
        // Fill dp[][]
        for(int i = 1; i < length; i++){
            for(int j = 0; j < length; j++){
                int pathSum1 = (j > 0) ? dp[(i-1)&1][j-1] : Integer.MAX_VALUE;
                int pathSum2 = dp[(i-1)&1][j];
                int pathSum3 = (j < length-1) ? dp[(i-1)&1][j+1] : Integer.MAX_VALUE;
                dp[i&1][j] = Math.min(Math.min(pathSum1, pathSum2), pathSum3) + matrix[i][j];
            }    
        }
        // Find result
        int res = Integer.MAX_VALUE;
        for(int i = 0; i < length; i++){
            if(dp[(length-1)&1][i] < res) res = dp[(length-1)&1][i];
        }
        return res;
    }
}

🔴 1289. 下降路径最小和 II

给你一个整数方阵 arr ，定义「非零偏移下降路径」为：从 arr 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

请你返回非零偏移下降路径数字和的最小值。

示例 1：

输入：arr = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

提示：

• 1 <= arr.length == arr[i].length <= 200
• -99 <= arr[i][j] <= 99

题解

这题非常适合 DP 练习。首先可以依照正常 DP 思路解之：

• 状态定义：dp[i][j] 表示移动到位置 (i,j) 的最小路径和，且显然初始条件为 dp[0][:] = matrix[0][:]，表示第一行各节点到自己的最短路径和即为自己本身。
• 状态转移：由题意可知，dp[k] 可由上行除了正上方之的任意节点转移来，因此选择上层除正上方外的最小的那个 DP 节点进行转移即可。

完整代码：

class Solution {
    int MAX = Integer.MAX_VALUE;
    public int minFallingPathSum(int[][] grid) {
        int length = grid.length;
        int[][] dp = new int[2][length];
        // Initialize dp
        for(int i = 0; i < length; i++) dp[0][i] = grid[0][i];
        // Fill dp
        for(int i = 1; i < length; i++){
            for(int j = 0; j < length; j++){
                // Find minimal dp in last layer except the dp directly above
                int minLastDp = MAX;
                for(int k = 0; k < length; k++){
                    if(k == j) continue;
                    if(dp[(i-1)&1][k] < minLastDp) minLastDp = dp[(i-1)&1][k];
                }
                // Update current dp
                dp[i&1][j] = minLastDp + grid[i][j];
            }
        }
        // Find result
        int res = MAX;
        for(int i = 0 ; i < length; i++){
            if(dp[(length-1)&1][i] < res) res = dp[(length-1)&1][i];
        }
        return res;
    }
}

不过由于转移来源范围太广了，导致算法的时间复杂度直接飙到了 $O(n^3)$，虽然能 AC，但实在不够优雅。为了降低时间复杂度，还是少偷点懒吧。

其实很容易发现，下一层将使用到的 dp 在遍历当前层的时候就可以被基本确定下来，因为下层 dp 期待的是由上层最小的 dp 转移来，那么只需要记录当前层最小的两个 dp 值供下层用就行了。

为什么是两个呢？Obviously，最小的那一个可能恰好处于下层遍历节点的正上方，这样的话最小的上层 dp 就不能用了，而如果最小的在正上方，那么第二小的就一定不在正上方，因此转移到下层的 dp 必然是当前层最小的那两个 dp 值当中的一个。

由于下层找转移来源的时候不需要再遍历整个上一层了，时间复杂度也就降到了 $O(n^2)$，执行用时从 45ms 优化到了 4ms，效果还算不错。

class Solution {
    int MAX = Integer.MAX_VALUE;
    public int minFallingPathSum(int[][] grid) {
        int length = grid.length;
        int[][] dp = new int[2][length];
        int smallestIndex = -1, secondSmallestIndex = -1;
        // Initialize dp and 1st, 2nd smallest index
        for(int i = 0; i < length; i++) {
            dp[0][i] = grid[0][i];
            // Update 1st, 2nd smallest index
            if(smallestIndex == -1 || grid[0][i] <= grid[0][smallestIndex]){
                secondSmallestIndex = smallestIndex;
                smallestIndex = i;
            }
            else if(secondSmallestIndex == -1 || grid[0][i] <= grid[0][secondSmallestIndex])
                secondSmallestIndex = i;
        }
        // Fill dp
        for(int i = 1; i < length; i++){
            // save 1st, 2nd smallest index of current layer
            int curSmallest = 0, curSecSmallest = 0;
            for(int j = 0; j < length; j++){
                // If the smallest dp directly above the node, then use the second smallest dp of above layer
                dp[i&1][j] = ((smallestIndex!=j)?dp[(i-1)&1][smallestIndex]:dp[(i-1)&1][secondSmallestIndex]) + grid[i][j];
                // Update 1st, 2nd smallest index of current layer
                if(dp[i&1][j] <= dp[i&1][curSmallest]){
                    curSecSmallest = curSmallest;
                    curSmallest = j;
                }
                else if(dp[i&1][j] <= dp[i&1][curSecSmallest])
                    curSecSmallest = j;
            }
            // Switch 1st, 2nd smallest index from above layer to current layer
            smallestIndex = curSmallest;
            secondSmallestIndex = curSecSmallest;
        }
        // The result is the smallest dp in current layer after the last dp layer filled
        return dp[(length-1)&1][smallestIndex];
    }
}

且慢！

仅仅这样就可以了吗？

可以看到，经过上面的优化后，我们实际只用到了每层最小的那两个 dp 而已，其它的数据都并没有用到，那么为什么还要白画 $O(n)$ 的空间复杂度去存储这些用不到的 dp 值呢？因此我们可以将优化后的“残垣断壁”清理一下了，至只存储当前层最小的两个 dp，其它数据一概不要，这样直接将空间复杂度压到了 $O(1)$。

同时，尽管此举的目的是优化空间，但由于之前离散地访问二维数组，空间局部性很差，经过空间优化取消了数组直接用整型变量存储需要的最小和次小 dp 后，执行用时受益，进一步大大降低到了 2ms。

class Solution {
    int MAX = Integer.MAX_VALUE;
    public int minFallingPathSum(int[][] grid) {
        int smallest = MAX, secondSmallest = MAX;
        int smallestIndex = 0;
        // Initialize dp and 1st smallest index
        for(int i = 0; i < grid.length; i++) {
            if(grid[0][i] <= smallest){
                smallestIndex = i;
                secondSmallest = smallest;
                smallest = grid[0][i];
            }
            else if(grid[0][i] <= secondSmallest) secondSmallest = grid[0][i];
        }
        // Fill dp
        int curSmallest, curSecSmallest;
        int curSmallestIndex;
        for(int i = 1; i < grid.length; i++){
            curSmallest = curSecSmallest = MAX;
            curSmallestIndex = 0;
            for(int j = 0; j < grid.length; j++){
                // If the smallest dp directly above the node, then use the second smallest dp of above layer
                int dp = ((smallestIndex!=j)?smallest:secondSmallest)+grid[i][j];
                // Update 1st, 2nd smallest dp of current layer
                if(dp <= curSmallest){
                    curSmallestIndex = j;
                    curSecSmallest = curSmallest;
                    curSmallest = dp;
                }
                else if(dp <= curSecSmallest) curSecSmallest = dp;
            }
            // Switch 1st, 2nd smallest dp from above layer to current layer
            smallestIndex = curSmallestIndex;
            smallest = curSmallest;
            secondSmallest = curSecSmallest;
        }
        return smallest;
    }
}

---

回溯遍历

🟠 22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

有效括号组合需满足：左括号必须以正确的顺序闭合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

• 1 <= n <= 8

题解

使用回溯遍历的方式，不断对当前状态追加可能的括号。

• 初始时左右括号余量均为 n；
• 当左括号有余量时，可以加入左括号；
• 当右括号有余量且余量大于左括号的余量时，可以加入右括号；
• 当左右括号都无余量时，一个合法的括号组合构造完毕，递归结束。

完整代码：

class Solution {
    List<String> res;
    public List<String> generateParenthesis(int n) {
        res = new ArrayList<String>();
        addParenthesis(new StringBuilder(), n, n);
        return res;
    }
    public void addParenthesis(StringBuilder builder, int left, int right){
        if(left == 0 && right == 0)  res.add(builder.toString());
        if(left > 0){
            builder.append('(');
            addParenthesis(builder, left-1, right);
            builder.deleteCharAt(builder.length()-1);
        }
        if(right > 0 && right > left){
            builder.append(')');
            addParenthesis(builder, left, right-1);
            builder.deleteCharAt(builder.length()-1);
        }
    }
}

---

DFS + 剪枝

🔴 301. 删除无效的括号

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按 任意顺序 返回。

示例 1：

输入：s = "()())()"
输出：["(())()","()()()"]

示例 2：

输入：s = "(a)())()"
输出：["(a())()","(a)()()"]

示例 3：

输入：s = ")("
输出：[""]

提示：

• 1 <= s.length <= 25
• s 由小写英文字母以及括号 '(' 和 ')' 组成
• s 中至多含 20 个括号

题解

因为每一个半括号都有可能被删除，因此首先考虑用回溯遍历解决本题。在每一个下标处，如果对应字符是括号，那么就可以选择保留，也可以选择不保留，直到字符串的最后一个字符扫描完毕，检查其是否构成一个有效的串，

如何检查其括号是否有效呢？非常简单，只需设置一个偏移变量 bias 记录左括号的盈余状态

• 若扫描并加入了一个左括号，则 bias++
• 若扫描并加入了一个右括号，则 bias--

那么显然在扫描的途中，一旦出现 bias < 0 则说明串已经出现非法状态，必然无效，不需要再往后扫描了，此时可以剪枝。而在整个串扫描完毕后，检查 bias 的值即可，若为 0 则说明没有左括号盈余，也就是有效，否则无效。

不过这样的遍历耗时还算非常严重的，经过分析思考不难发现仍有可剪枝的地方。由于题目要求删除最小数量的括号，这就给优化提供了一条思路，即在 DFS 的过程中记录前面已经删除的括号数量，若在递归过程中删除的括号数量已经大于了之前产生过的有效串所删除的括号数，那么就不必再往深处遍历了，就算再找到有效串，也必然不是删除最小数量括号的串，不能作为结果之一。

完整代码：

class Solution {
    List<String> res;
    int minRemoved = Integer.MAX_VALUE;
    public List<String> removeInvalidParentheses(String s) {
        res = new ArrayList<>();
        minRemoved = Integer.MAX_VALUE;
        buildRes(s, 0, new StringBuilder(), 0, 0);
        int maxLength = -1;
        // 找到删除括号最小的串的长度
        for(int i = 0; i < res.size(); i++){
            if(res.get(i).length() > maxLength) maxLength = res.get(i).length();
        }
        // 只保留与删除括号最小串长度相同的串作为答案
        for(int i = 0; i < res.size(); i++){
            if(res.get(i).length() != maxLength) res.remove(res.get(i--));
        }
        return res;
    }
    public void buildRes(String s, int index, StringBuilder sb, int bias, int removed){
        // 当前删除的括号数若已经超过了已有的有效串所删除的括号数，则剪枝
        if(removed > minRemoved) return; 
        // 遍历到末尾，检查串是否有效、串是否已存在结果集中
        if(index == s.length()){
            if(bias == 0 && !res.contains(sb.toString())){ 
                res.add(0, sb.toString());
                // 更新构成有效串可删除的最小括号数
                if(removed < minRemoved) minRemoved = removed;
            }
            return;
        }
        char current = s.charAt(index);
        // 非括号元素不能删除，直接添加
        if(current != '(' && current != ')'){
            sb.append(current);
            buildRes(s, index + 1, sb, bias, removed);
            sb.deleteCharAt(sb.length() - 1);
            return;
        }
        // 若中途 bias<0 则说明必构成无效串，剪枝
        if(bias + (current == '(' ? 1 : -1) >= 0){
            // bias 合法，录用该括号字符
            sb.append(current);
            buildRes(s, index + 1, sb, bias + (current == '(' ? 1 : -1), removed);
            sb.deleteCharAt(sb.length() - 1);
        }
        // 不录用(删除)该字符
        buildRes(s, index + 1, sb, bias, removed + 1);
    }
}

---

双指针

🟠 11. 盛最多水的容器

给你 n 个非负整数 a1，a2，...，a``n，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

示例 1：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 10^5
• 0 <= height[i] <= 10^4

题解

最容易想到的当然是遍历所有可能垂线组合的暴力法了，不过注意到 n <= 10^5 的数据范围，显然 $O(n^2)$ 的搜索办法是会超时的。本题可以使用双指针的思想来解决。首先将两个指针分别置于两侧的垂线处，考虑到若将较长的垂线向内侧移动的话，面积必然变小，因此较短一侧能够产生的最大面积必然就是当前时刻的面积，其不可能再提供更大的面积了，因此可以直接舍弃较短侧的垂线，将短侧向内移动，按此规则不断移动，则能够记录下所有的垂线能产生的最大面积，那么答案就必然在这个“所有垂线能产生的最大面积”的集合中，因此，只需利用双指针移动遍历依次，记录过程中产生的最大面积值即是本题的答案。

完整代码：

class Solution {
    public int maxArea(int[] height) {
        int max = 0;
        int i = 0, j = height.length - 1;
        while(i < j){
            int area = (j - i) * Math.min(height[i], height[j]);
            if(area > max) max = area;
            if(height[i] <= height[j]) i++; else j--;
        }
        return max;
    }
}