Tensorflow 2.3 入门与实战笔记 02 —— 线性回归与梯度下降

作者 Sunwish | 发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

概述

本文记录了 Tensorflow 中线性回归的实现方法及如何使用梯度下降算法，仅为框架用法，其理论与底层实现不做介绍，有需要请移步往期深度学习专题博文，搭配食用更佳 深度学习（一）Logistics 回归与梯度下降。

Title

一、准备工作

1. 包

确保你已经安装好 tensorflow 及接下来会使用到的包 pandas 及 matplotlib。

2. Jupyter notebook

打开 Jupyter notebook 新建一个 Python 3 文件以编写与测试代码。

3. 数据

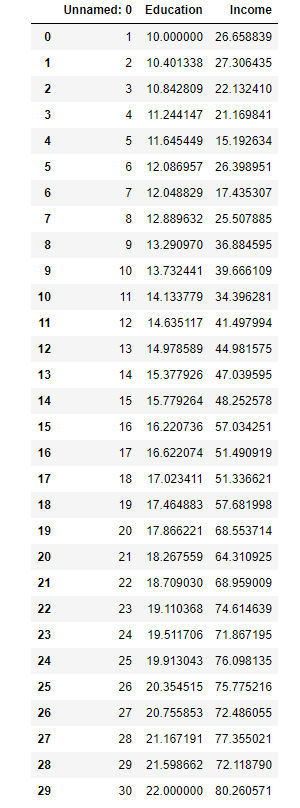
本篇以受教育年数与工作收入作为模型训练数据，以期实现一个由受教育年数来预测工作收入的简单模型。将以下数据放入记事本中，改后缀为 Income.csv 得到测试用数据，将文件放在新建的 Python 3 文件的同级目录或方便读取的目录。

二、读入数据

1
2
3
4
5
6
# 导入 pandas 包用于读取 csv 数据
import pandas as pd
# 读取 csv 数据
data = pd.read_csv("Income.csv")
# 输出读取得到的数据
data

由 图2-1 输出可知数据包含两列，分别是 Education 与 Income。

输出data数据

图 2-1 输出内容
1
2
3
4
5
6
7
# 导入 matplotlib 包用于数据可视化
import matplotlib.pyplot as plt
# 内联显示
%matplotlib inline

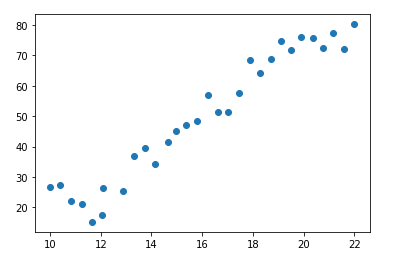
# 绘制 data 散点图，以 data.Education 为横坐标，data.Income 为纵坐标
plt.scatter(data.Education, data.Income)

由 图2-2 可知分别以 Education 和 Income 为横轴坐标轴的数据分布基本呈现线性关系。

data散点图

图 2-2 data 散点图

三、模型搭建与训练

1. 创建模型实例

1
2
3
4
# 建立序贯模型（最简单的线性），返回一个 Model 实例
model = tf.keras.Sequential()
# 向模型添加层
model.add(tf.keras.layers.Dense(1, input_shape=[1]))

其中 tf.keras.layers.Dense() 返回一个常规的神经网络层（NN Layer），其第一个参数为 unit 正整数，指明输出矩阵维度，此处 1 表明该层的输出是 $\n times 1$ 的。

第二个参数 input_shape 指明输入形状，input_shape=[1] 指明输入样本的特征数为 1（此例输入即 data.Education），而该层输入参数是 2 个（应该分别是一维的权重 $w$ 和偏置 $b$ 吧）。

此外，查官方文档可知 input_shape 参数继承自 Layer 类，其实质是一个 TensorShape 类型的实例。

因此也可写作 model.add(tf.keras.layers.Dense(1, input_shape=tf.TensorShape([1])))

此外，Dense 层也有其他参数，如可在构造函数中为 activation 赋值以指明本层激活函数，详细可以去看看文档。

1
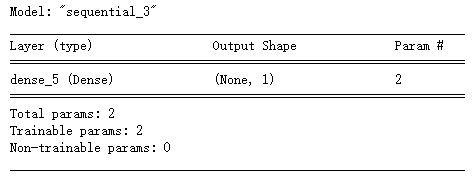
2
# 输出此时模型信息
model.summary()

使用 summary 可以看出，此时 model 拥有了一个 Layer，这个 layer 的输出形状是 $None \times 1$ 的。经查阅 Tensorflow 官方文档，tf 中的输入输出形状均描述为形如 (batch_size, ..., input/output_dim) 的结构，即输出形状 $m \times n$ 的意义是 $m$ 个样本的输出，每个样本的输出维度为 $n$，这与往期深度学习博文中的抽象数学定义也是相符的。None 猜测一下应该是表示输出数待定，待定为我们输入样本的个数。

model summary

图 2-2 Model summary

2. 配置模型

1
2
# 编译模型
model.compile(optimizer='adam', loss='mse')

在训练模型之前还需对模型进行一些配置，例如指明优化方法、损失函数等，compile 就是用于指明这些配置，详细的可配置参数请移步 compile 函数文档。

optimizer 指明优化方法，该参数接受优化方法名，也接受优化方法的实例（tf.keras.optimizers），adam 即使用梯度下降作为优化方法。

loss 指明 LossFunction，同样接受损失函数名或损失函数实例（tf.keras.losses），mse 即使用均方差作为损失函数。

3. 训练模型

1
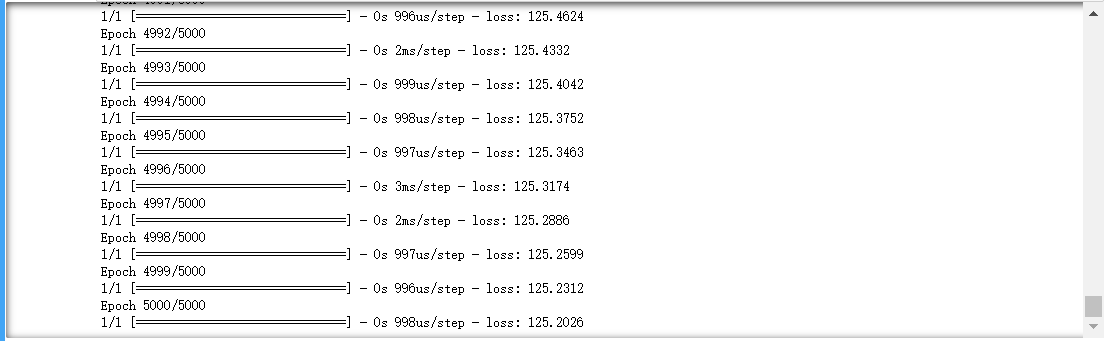
2
# 以 data.Education 和 data.Income 作为输入参数，训练模型 5000 轮
history = model.fit(data.Education, data.Income, epochs=5000)

详细可选参数移步官方文档：tf.keras.Model.fit

fit history

图 2-2 Fit history

四、模型预测

1
2
# 使用刚才训练好的模型对训练集进行预测
pd = model.predict(data.Education)
1
2
3
4
# 计算预测值与真实值之间的差距
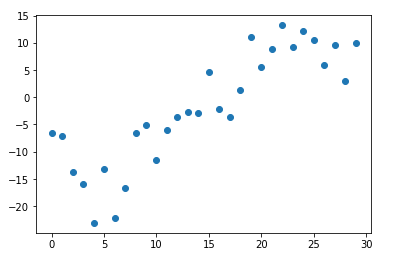
delta = []
for i in range(len(data.Income.values)):
    delta.append(data.Income.values[i] - pd[i])
1
2
# 绘制差距图
plt.scatter(list(range(0, len(delta))), delta)

delta

图 2-2 Delta
如果你觉得文章内容对你有帮助，可以打赏支持一下哦！

0%