深度学习（三）实战：动手实现猫图识别

作者 Sunwish | 发表于 | 更新于 | 分类于 ， | 评论数： | 阅读次数：

概述

本篇详细记录了如何使用 Python 语言基于 Logistic 回归搭建一个简单的单层神经网络，并实现猫图的识别。
本篇中的单层神经网络在训练集与测试集上分别获得了 95.7% 与 74.0% 的正确率。

Title

本篇将在 Jupyter Nootbook 中使用 Python 语言进行编程。

简单来说， Jupyter 是一个交互式笔记本，可以在一个 Jupyer 笔记本文件中同时记录 Markdown 笔记与添加可分段执行的代码块。

Jupyter Notebook 是一个基于网页的用于交互计算的应用程序。其可被应用于全过程计算：开发、文档编写、运行代码和展示结果。（摘自官方介绍）

Jupyter Notebook（此前被称为 IPython notebook）是一个交互式笔记本，支持运行 40 多种编程语言。Jupyter Notebook 的本质是一个 Web 应用程序，便于创建和共享文学化程序文档，支持实时代码，数学方程，可视化和 markdown。 用途包括：数据清理和转换，数值模拟，统计建模，机器学习等等。（摘自百度百科）

3.0 数据导入

本篇使用的数据摘自吴恩达深度学习课程，可以在本篇末尾获取下载。在搭建神经网络之前，不如先看一看数据是怎样的。

1
2
from lr_utils import load_dataset
train_X_orig, train_Y, test_X_orig, test_Y, classes = load_dataset()

其中 load_dataset 就将数据进行了导入，如果你好奇数据是怎么导入的，可以点开下面的隐藏块查看代码细节，但是目前为止你并不需要关心数据是怎么导入的，以及数据来源是什么，因为这些都不是本篇的重点，你要关注内容的应该是神经网络在编程中到底是如何实现的，当你真正实现了你的神经网络之后，只需要将数据按照你的网络需要进行格式处理并输入就行了。在本篇当中你直接将数据下载下来并使用上面的一行代码导入进行使用即可。

导入数据后的第一件事情，应该关心数据的存储结构，下面几行代码输出了训练集输入（train_set_x_orig）、训练集输出（train_set_y）、测试集输入（test_set_x_orig）及测试集输出（test_set_y）的形状。

1
2
3
4
print ("Shape of train_set_x_orig: " + str(train_set_x_orig.shape))
print ("Shape of train_set_y: " + str(train_set_y.shape))
print ("Shape of test_set_x_orig: " + str(test_set_x_orig.shape))
print ("Shape of test_set_y: " + str(test_set_y.shape))

输出结果是：

    Shape of train_X_orig: (209L, 64L, 64L, 3L)
    Shape of train_Y: (1L, 209L)
    Shape of test_X_orig: (50L, 64L, 64L, 3L)
    Shape of test_Y: (1L, 50L)

由此不难获得几点信息：

  • 训练集中有209个训练元素；测试集中有50个测试元素。
    即 $m{train} = 209$, $m{test} = 50$。

  • 训练集和测试集的图像宽高均为 $64 \times 64$。

而 $3L$ 代表的是 $RGB$ 三通道。如果对图像在计算机当中的存储形式有所了解的话，应该对 $RGB$ 不陌生，电脑屏幕上的所有颜色，都由这红色(R)绿色(G)蓝色(B)三种色光按照不同的比例混合而成。

通过 matplotlib.pyplot 中提供的 imshow 函数可以将一幅 RGB 图像显示出来：

1
2
3
4
5
6
import matplotlib.pyplot as plt

# 显示训练集中的第 index 个训练图像
index = 102
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[int(train_set_y[:, index])] +  "' picture.")

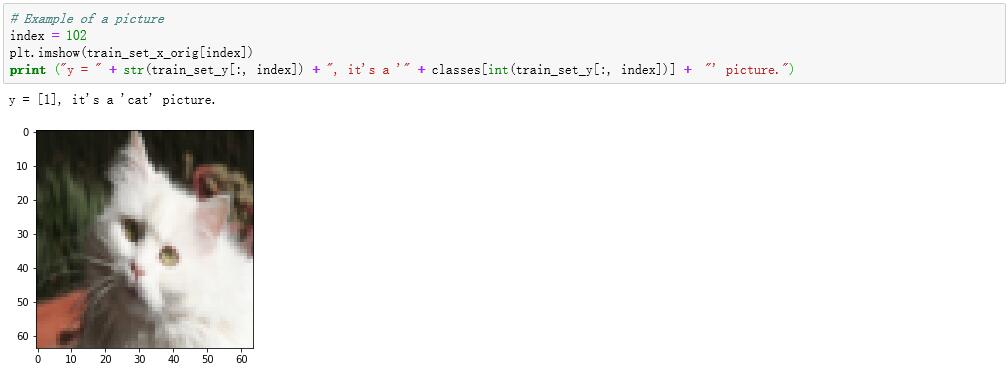
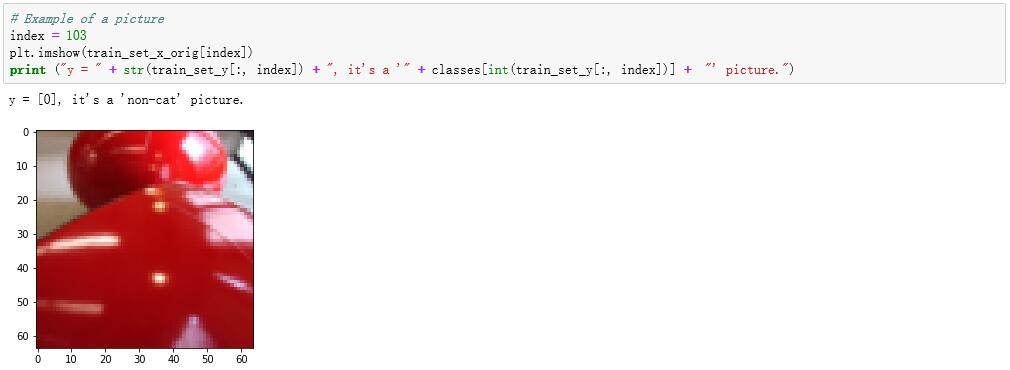
Title

图 1-1 使用 imshow 函数显示图像

可以看到，在训练集中的第103个样本图像是一张猫图。其中输出的结果 “y = [1]” 表示这张图片的标注是 “1”，也就表示 “是” 的意思。不妨再看一看第104个样本，可以看到不是猫图，而对应的输出结果也变成了 “y = [0]”。

Title

图 1-2 使用 imshow 函数显示图像

3.1 数据处理

在前面已经完成了数据集的导入，并且查看了训练集当中的两个样本图像及对应的图像标注。但是这些数据目前为止还不方便我们使用，下面看一看如何将其调整为合适的格式。

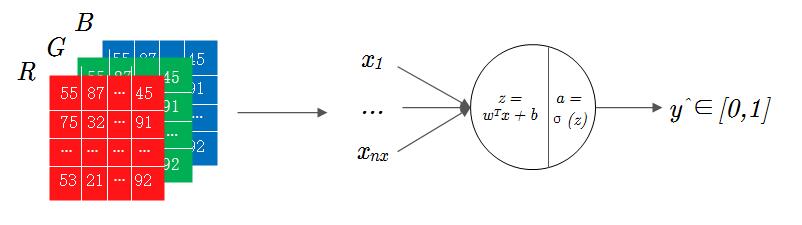
对于单个训练样本而言，所有的输入按照列矩阵的形式传入网络，即输入 $x$ 的是 $n_x \times 1$ 维的矩阵，但是一幅 $64 \times 64$ 图像的在数据集中是以 $64 \times 64 \times 3$ 的矩阵形状进行存储的，为了满足神经网络的输入格式，在 Python 中可以使用 reshape 函数改变矩阵的形状，对于一个形状为 $(a,b,c,d)$ 的矩阵 $M_1$ 而言，通过 $M_1.reshape(M_1.shape[0],-1).T$ 就可以将其转换为形状为 $(b \times c \times d,a)$ 的矩阵了。

其中第一项参数 $M_1.shape[0]$ 表示的就是 $M_1$ 原来的第一维长度 $a$，第二项参数 $-1$ 表示将后面的所有维度堆叠成一个维度，这样就得到了一个形为 $(a,b \times c \times d)$ 的矩阵，再通过”.T”进行转置，就得到了 $a$ 个列矩阵堆叠得到的“向量化矩阵”。

使用这个方法就可以对数据集中的图像数据进行降维处理了：

1
2
3
4
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T
print ("Shape of train_set_x_flatten: " + str(train_set_x_flatten.shape))
print ("Value of test_set_x_flatten: " + str(test_set_x_flatten))

输出结果：

    Shape of train_set_x_flatten: (12288L, 209L)
    Value of test_set_x_flatten: [[158 115 255 … 41 18 133]
     [104 110 253 … 47 18 163]
     [ 83 111 254 … 84 16 75]
     …
     [173 171 133 … 183 144 5]
     [128 176 101 … 141 137 22]
     [110 186 121 … 116 108 5]]

其中按列看，每一列代表一个样本图像的所有 $RGB$ 数值，共有209个训练样本，因此 train_set_x_flatten 有209列。

数字 12288 是 RGB 全部铺平的数值总量
因为图片是 $64×64$ 的，因此 $R、G、B$ 各有 $64×64=4096$ 个值，$RGB$ 共三层，$4096×3=12288$。

单个样本的RGB颜色值在 flatten 当中应该是这样存放的：

至此，我们完成了数据集的格式化处理，即 图1-3 中左侧RGB图像到右侧输入层的转换。

Title

图 1-3 输入数据格式化

不过，imshow()显示图像时对double型是认为在0~1范围内，因此再将颜色值全部除以255将值转换到0~1。

1
2
3
4
train_set_x = 1.0*train_set_x_flatten/255
test_set_x = 1.0*test_set_x_flatten/255
print ("Shape of train_set_x: " + str(train_set_x.shape))
print ("Value of test_set_x: " + str(test_set_x))

输出结果：

    Shape of train_set_x: (12288L, 209L)
    Value of test_set_x: [[0.61960784 0.45098039 1. … >     0.16078431 0.07058824 0.52156863]
     [0.40784314 0.43137255 0.99215686 … 0.18431373 0.07058824 0.63921569]
     [0.3254902 0.43529412 0.99607843 … 0.32941176 0.0627451 0.29411765]
     …
     [0.67843137 0.67058824 0.52156863 … 0.71764706 0.56470588 0.01960784]
     [0.50196078 0.69019608 0.39607843 … 0.55294118 0.5372549 0.08627451]
     [0.43137255 0.72941176 0.4745098 … 0.45490196 0.42352941 0.01960784]]

现在，整个数据集的输入数据都已经处理好了放在矩阵 train_set_x 与 test_set_x 当中，形式如下：

如果你有些忘记了上面这个矩阵的行数、列数及每一个角标的意义的话，请回看上一篇向量化的第一节，里面有详细的解释，不过结合矩阵的角标你应该很好理解了。

至此，训练和测试数据都有了并且都规范好了，正式开始搭建你的神经网络吧！

3.2 搭建神经网络

numpy

在开始写代码之前，你需要先导入一下 numpy：

1
import numpy as np

numpy 是 Python 的一种开源的数值计算扩展，这种工具可用来存储和处理大型矩阵，在上一篇向量化当中所记录的是如何将 Logistic 回归向量化，即将循环代码转换为矩阵计算的形式，而 numpy 就可以帮助你实现矩阵的相关计算。

例如现在将定义一个函数 sigmoid 用于计算所有输入样本 $z$ 值的 $\sigma$ 函数值：

1
2
3
4
5
# sigmoid 函数

def sigmoid(z):
    a = 1./(1+np.exp(-z))
    return a

np.exp 是 numpy 提供的求自然指数的函数，对如输入参数为矩阵的时候，会对矩阵中的所有元素求自然指数，如果不使用 numpy 的话，你就要写一个大的 for 循环来遍历所有的数据并计算了，在上一篇中你已经看到了 for 循环的效率是很低的，这就是使用 numpy 的必要性，即向量化计算的落地实现。

初始化参数

下面定义的函数 initialize_parameters 用于初始化参数 $w$ 和 $b$，传入输入的维数，返回一个值为 0 的 $b$ 及对应维数的 $w$。

np.zeros((a,b))，用于生成一个形状为 $a \times b$ 的零矩阵。 

1
2
3
4
5
6
7
# Initialize parameters

def initialize_parameters(dim):
    w = np.zeros(shape=(dim, 1), dtype=np.float32)
    b = 0
    
    return w, b

向前/后传播

下面定义的函数 propagate 将完成一次向前传播与向后传播。

如果对下面代码理解还有困难的话，其中向前传播的 Cost Function 见 第一篇 中的1.2节，向后传播中 $dw$ 与 $db$ 见 第一篇 中公式(24)(25)，对向量化形式的不清楚请回看 第二篇。

np.sum(M)，是 numpy 中的求和函数，可以对矩阵按行/列进行堆叠求和，参数 axis = 1 时表示按行求和。
np.dot(M1,M2)，是 numpy 中的点乘函数，用于对两个矩阵做点乘运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def propagate(w, b, X, Y):
    
    m = X.shape[1]
    
    # 向前传播
    A = sigmoid(np.dot(w.T,X) + b)
    
    cost = (-1./m) * np.sum((Y*np.log(A) + (1-Y)*np.log(1-A)), axis = 1) # axis = 1 代表按行求和
    
    # 向后传播
    dw = (1./m)*np.dot(X, ((A-Y).T))
    db = (1./m)*np.sum(A-Y, axis = 1)
    
    cost = np.squeeze(cost) # trans cost from matrix 1x1 into a real number
    
    return dw, db, cost

梯度下降

下面的函数 optimized 将实现梯度下降，参数 train_times 和 learning_rate 分别用于设定训练次数及学习率。变量 costs 用于记录参数 $w$、$b$ 对应的成本函数值，每训练100次记录一次成本，用于后期绘制 costs 关于训练次数的变化图像，以了解模型的学习情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def optimized(w, b, X, Y, train_times, learning_rate):
    
    costs = []
    
    for i in range(train_times):
        
        dw, db, cost = propagate(w, b, X, Y)

        # 参数迭代
        w = w - learning_rate * dw
        b = b - learning_rate * db
        
        # 记录成本函数
        if i%100 == 0:
            costs.append(cost)
        
    return w, b, costs

输入预测

下面的函数 predict 用于输入预测，其实也就是计算一次向前传播，得到输出结果就是预测值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def predict(w, b, X):
    
    m = X.shape[1]
    Y_prediction = np.zeros((1,m))
    
	# 确保矩阵维数匹配
    w = w.reshape(X.shape[0], 1)
    
	# 计算 Logistic 回归
    A = sigmoid(np.dot(w.T, X) + b)
	
	# 如果结果大于0.5，打上标签"1"，反之记录为"0"
    for i in range(A.shape[1]):
        if A[0, i] > 0.5:
            Y_prediction[0, i] = 1
        else:
            Y_prediction[0, i] = 0
    
	# 确保一下矩阵维数正确
    assert(Y_prediction.shape == (1,m))
    
    return Y_prediction

模型封装

在前面我们已经将模型的主体即向前传播向后传播和梯度下降都模块化地完成了，接下来把这些步骤拼接在一起得到最终的模型吧！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def TestMyModel(X_train, Y_train, X_test, Y_test, train_times = 100, learning_rate = 0.005):
    
    # 初始化参数
    w, b = initialize_parameters(X_train.shape[0])
    
    # 开始梯度下降训练
    w, b, costs = optimized(w, b, X_train, Y_train, train_times, learning_rate)
    
    # 训练完成，测试一下效果
    Y_prediction_train = predict(w, b, X_train)
    Y_prediction_test = predict(w, b, X_test)
    
    # 输出效果
    print("Accuracy on train_set: " + str(100 - np.mean(np.abs(Y_prediction_train-Y_train)) * 100) + "%")
    print("Accuracy on test_set: " + str(100 - np.mean(np.abs(Y_prediction_test-Y_test)) * 100) + "%")
    print(Y_prediction_test)
    return w, b, costs, Y_prediction_test

3.3 效果测试

数据集测试

至此，你已经完成了一个单层神经网络的构建，让我们来测试一下效果吧！

1
2
3
w, b, costs, Y_prediction_test = TestMyModel(train_set_x, train_set_y, test_set_x, test_set_y, 2000, 0.002)
plot_costs = np.squeeze(costs)
plt.plot(plot_costs)

输出结果：

Accuracy on train_set: 95.69377990430623%
Accuracy on test_set: 74.0%
[[1. 1. 1. 1. 1. 0. 0. 1. 1. 1. 0. 0. 1. 1. 0. 1. 0. 1. 0. 0. 1. 0. 0. 1. 1. 1. 1. 0. 0. 1. 0. 1. 1. 0. 1. 0. 0. 1. 0. 0. 1. 1. 1. 0. 1. 0. 0. 1. 1. 0.]]

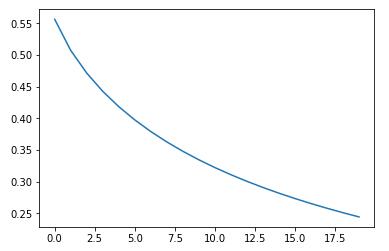
Title

图 1-4 成本函数关于训练次数图像

可以看到，对于学习率 0.002，训练2000次可以在训练集与测试集上分别得到 95.69% 与 74% 的正确率！这对于一个如此简单的单层神经网络来说已经算是不错了。

看看测试集中预测与图片的对比：

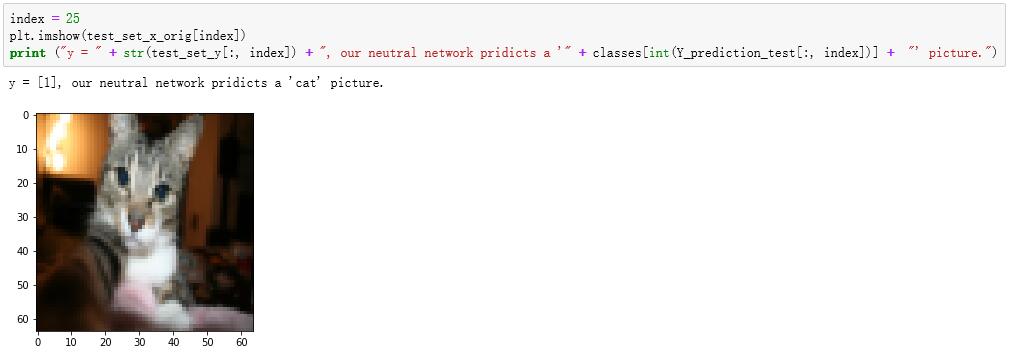
Title

图 1-4 测试集中预测与图片的对比

试试自己的数据

下面的函数 isCat 是对模型的进一步封装，用其来预测一张自定义的照片。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def isCat(my_image = "my_image.jpg", dirname = "images/"):

    # 初始化图片路径
    fname = dirname + my_image

    # 读取图片
    image = np.array(plt.imread(fname))

    # 将图片转换为训练集一样的尺寸
    num_px = train_set_x_orig.shape[2]
    my_image = skimage.transform.resize(image, output_shape=(num_px,num_px)).reshape((1, num_px*num_px*3)).T

    # 预测
    my_predicted_image = predict(w, b, my_image)

    # 绘图与结果输出
    plt.imshow(image)
    print("y = " + str(int(my_predicted_image)) + ", our neutral network predicts a \"" + classes[int(my_predicted_image),] +  "\" picture.")

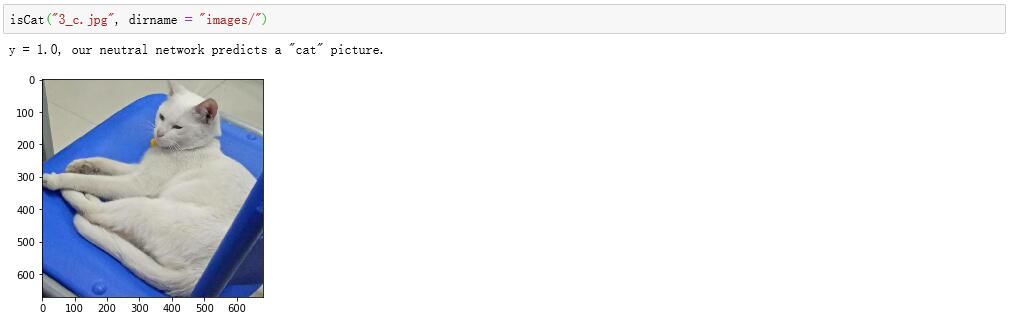
接下来我们试试识别自己拍的照片吧！

下面是我自己拍摄的一张白猫的照片，可以看到我们搭建的网络得到了正确的识别结果：

Title

图 1-4 识别自己拍摄的照片

如果你觉得文章内容对你有帮助，可以打赏支持一下哦！

0%