引言
在今天这个大数据的时代,我们当中的大部分人或许并没有海量的请求需要应对,但相信你总会遇到有大量数据需要处理的时候。为了在后期能够更加高效地对这些数据进行管理和操作,相信你一定不会愿意将宝贵的时间浪费在数据的搜索、查询和定位上。或许你应该掌握更加合理的数据处理办法,来提高你的程序及项目的运作效率。
一、什么是哈希表?
0x01 什么是哈希表?
哈希表是一种数据结构,它可以提供快速的插入操作和查找操作。
第一次接触哈希表时,它的优点多得让人难以置信。不论哈希表中有多少数据,查找、插入和删除(有时包括侧除)只需要接近常量的时间——0。对于常规的搜索定位方式来说,在巨量的数据中找到目标数据可能需要几十毫秒、几百毫秒甚至是按秒算,但在哈希表中查找不过是一瞬间的事。
为了更好地理解哈希表算法的基本原理,此处假定一个场景:Sun开发了一款即时通讯软件W,而Sun需要在W发布之前想好如何应对发布后越来越多用户的帐号操作请求(以搜索好友为例,为方便说明,简单假设数据均在程序数组内,不考虑数据库等外部因素)。于是Sun设想现在W已拥有100万活跃用户,数组A内存放了这些用户的数据。而此时某用户想要查询W号为66666的用户信息,如果你是Sun,你将如何在100万W号中找到66666,并返回其信息?
0x02 一般方法下的寻找过程?
在正式说到哈希之前,我们先来看一下没有相关经验的新人可能会使用的笨办法——直接遍历。
在遍历的过程中,程序首先查看A[1]内的W号,若不是66666则向下查看A[2],直到找到A[x]内的W号为66666,返回A[x]。
(注:本文中默认数据均从下标为1开始存储)
若足够幸运以至于A[1]就是66666,那么一步就完成了检索。若不凑巧A[100000]才是用户66666呢?那要花费多少时间和资源?这种方法虽然简单却有明显的缺陷,而这一类请求在今后是将高频出现的,有时候许多用户同时向服务器发起请求,显然不会得到理想的效果。
0x03 哈希表算法如何瞬间定位?
哈希表算法的高效率得益于数据存放的结构。让我们先来看一看一条数据是如何被放进哈希表当中的。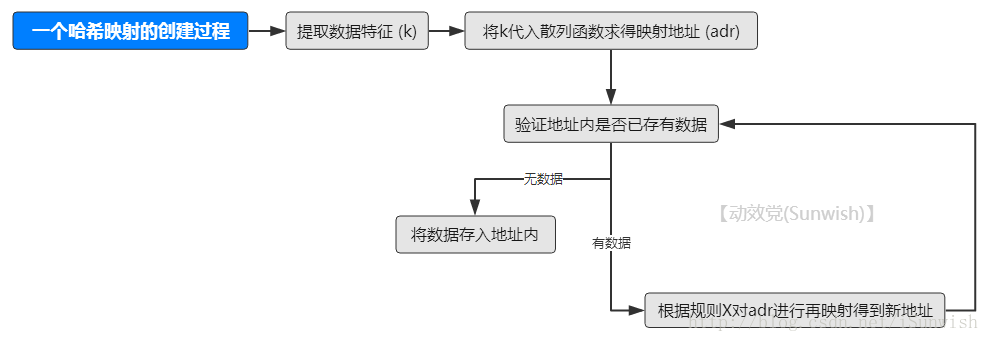
从上图可以看出,数据在哈希表中所存放的位置adr,是与数据本身具有函数映射关系的(即散列函数),也就是说我们依据某种规则,使得数据与其存放的地址之内能够相互转化,这样就无需盲目地从第一个找到最后一个,而是直接得到目标地址了!
二、初探哈希表算法
0x01 简单的例子及哈希表算法的弊端
举个例子,数组A={1, 3, 6, 13},哈希表为数组B,散列函数H(x)=2x,那么根据上图流程:
· A[1]在哈希表中的位置为12=2,
· A[2]在哈希表中的位置为32=6,
· A[3]在哈希表中的位置为62=12,
· A[4]在哈希表中的位置为132=26。
最终得到的哈希表:
· B[2] = 1
· B[6] = 3
· B[12] = 6
· B[26] = 13
其余的B[x]均为零。
那么当我们想要找13这个数据在哈希表中的位置时,我们不需要一个一个地试过去,而是直接得到地址adr=H(13)=26,即B[26]内存放了数据13。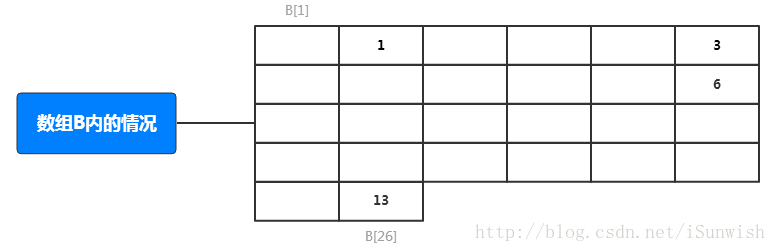
但由此我们就发现了空间的浪费,原本只有4个数据,而为了哈希表正常运作我们必须至少提供26个位置,也就是说有22个位置根本没有用到。可以说,哈希表算法就在是用空间换时间。为了得到更好的效果,我们必须牺牲许多在一般方法中不必要的空间,但在这个硬件越来越强大的时代,用空间换时间这一做法是绝对值得的。
0x02 寻求合适的散列函数
虽然哈希表算法有不可避免的空间浪费,但设定一个合适的散列函数可以大大地降低空间的浪费率。以上面的数组A为例,散列函数选为H(x)=2x时,哈希表空间的最大利用率为
可以说是非常低了。但如果我们以H’(x)=x%11(注:x除以11所得的余数)作为散列函数呢?我们将得到A[1]在B内的地址为1%11=1,以此类推,最终:
· B[1] = 1
· B[3] = 3
· B[6] = 6
· B[2] = 13
此时最小的哈希表只需要6个位置,其空间利用率变成了
